Courtesy of:
Willem Toet, Head of Aerodynamics,
Sauber F1 Team, Sauber Motorsport AG
Surface Finishes -
why are they not used on an F1 car
Aerodynamicists are often asked about ways to improve the performance of race cars using golf ball dimple effect, shark skin, riblets, super smooth surface finishes, bumble bee effect (hairy surfaces), etc. This is asked so often that we have decided to dedicate a small document to the subject, to explain some of these effects.
 |
Zipp Speed Weaponary, one of the world’s market leaders in racing bicycle wheels hold the world patent on dimpled disc cycle wheels, and they seem to work, being chosen by a number of top teams including some Tour de France front runners. Zipp use a roughly meniscus-shaped dimple with a flat bottom that sweeps upwards near the edges. Apparently this shape is popular in current golf ball design, particularly with manufacturer Titleist. |
Businesses exist and some even thrive on the promise of improved downforce / lift or reduced drag, or sometimes even both, using surface finish related treatments. We think surface finish is important but not as fundamental to race car performance as some people suggest. For some objects operating with different shapes and at different speeds, the importance can be much greater, eg a human swimmer, runner or cyclist (at one end – due to low speed mainly) and an aircraft (at the other end of the speed scale and due to skin friction drag). For different reasons surface finish can be very important.
F1 cars operate with many different flow states, including the following:
- Laminar (efficient, powerful, ideal but potentially unstable and rarely seen for any length of a surface on an F1 car for many reasons – e.g. surface imperfections caused by running for many laps in the real world, the extreme shapes employed in F1 to generate downforce, following other cars, etc.). Catastrophic flow separation is possible directly from laminar flow regions and laminar flow is easily disturbed by surface imperfections.
- Transition to... turbulent (less efficient in theory but more stable or more likely to ‘hang on’ to a curving surface). As turbulent flow is pushed more and more, sometimes a separation bubble starts to form (bubble implies that the flow attaches again further along the body). Sometimes off-body separations appear in the flow region while the flow still seems to be (just) attached ‘on-body’.
- Asymmetric 3D flow – i.e. remaining surface flow starts to go asymmetrical and sideways compared to global airflow direction – usually this is because one vortex of two has burst and usually some separation exists next to the asymmetric flow.
- Full separation of the flow from the body.
 |
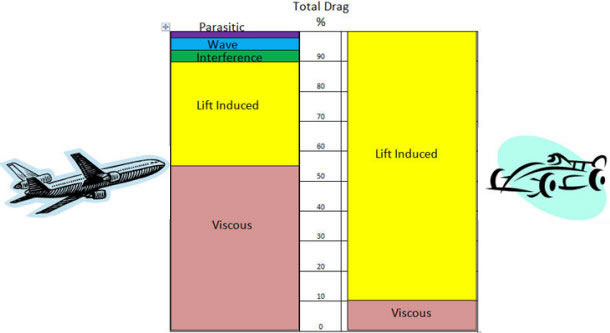Fig 1. Comparison of total drag of a plane vs an F1 car * |
The impact of golf ball dimples is going to be our primary focus but, when you have a clear understanding of this, it should be faster and easier to understand the impact of other surface treatments. The same concept of dimples is also used on some other sporting goods where it is possible to make a difference, sometimes quite big.
To explain we need to convey some basic principles because not all of this is simple. All other things being equal, the aerodynamic drag of an object increases with the square of speed (twice the speed means four times the drag force).
 |
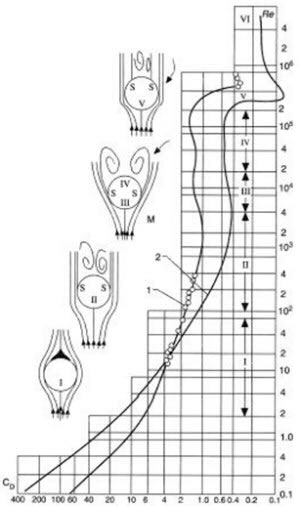Fig 2. Drag coefficients for cylinders (1) and spheres (2) as a function of Reynolds number (Re)** |
For this reason many objects (including cars) are often characterised with a drag coefficient or the drag coefficient x the frontal (or cross sectional) area for the body (i.e. the size of the body) and for simple checks these numbers can then be compared to see which body has more or less drag.
However, the drag coefficient of an object does not always remain the same as speed is changed, especially at quite low speeds or for small objects and for very high speeds (e.g. approaching the speed of sound). These changes in drag (coefficient) come about because the way the air behaves changes as speed and size are changed. Aerodynamicists, when talking about air speed and body size, talk about Reynolds numbers which is a non-dimensional number (basically speed x fluid [air] density x length of object ÷ viscosity of fluid [air]) that helps us to understand about boundary layer and flow types around the body.
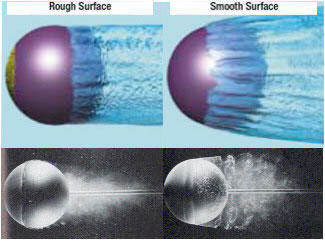
Golf balls have been scientifically compared to round spheres in a number of studies. One that I found useful gives the following graph of drag coefficient vs. Reynolds number (but you can think of this as drag coefficient vs. speed). From the graph you can see that the drag of a smooth and a rough sphere swap over as the Reynolds number changes. Given golf balls are used in atmospheric air and the balls are all the same size then we are talking about speed changes. At some speeds the smooth sphere will have less drag – at some speeds the smooth sphere will have more drag. The difference can be above 25 % of the drag of the object in a given set of conditions.
 |
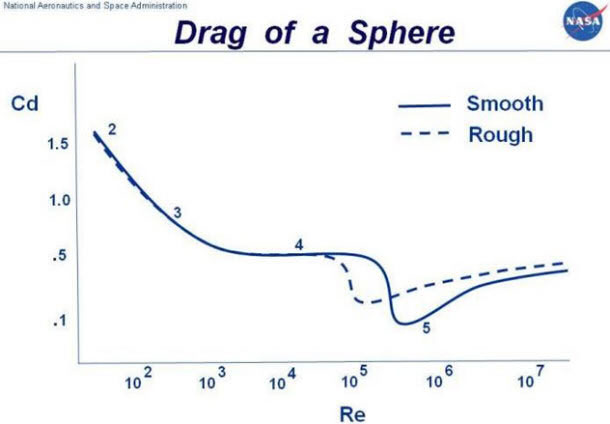Fig 3. Plot of drag coefficient v Reynolds number for a smooth and rough surface sphere (courtesy of http://www.grc.nasa.gov/WWW/k-12/airplane/dragsphere.html) |
For comparison, going from a cylinder to an aerofoil, the drag (again depending on speed and scale) goes from a coefficient of drag of above 1.0 for the cylinder (except at high speed or scale) to a drag coefficient of less than 0.1 for an aerofoil called a NACA 0030. This over 90% reduction makes a 25% reduction in drag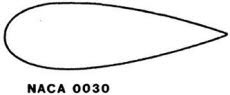 
seem small by comparson. Suspension elements on Formula 1 cars are regulated to have maximum aspect ratios a bit like the sketch here. This means that, for a car designer, thinking about global shape changes is likely to be more interesting in terms of drag changes than thinking about special surface details. Aerodynamicists in the aircraft industry and even those in automotive quickly realised, after early experiments, that working on the overall shape was more productive than experimenting with surface finishes. In normal operation on a road car, skin friction accounts for no more than 1 percent of the total drag since the main drag generation mechanism is the vehicle shape. Ford experimented with the sharkskin wrap in the mid 80s when they developed a low-drag Probe IV concept car which had a Cd of 0.15. They did not see improvements in drag so moved on to work with the vehicle shape. ***
 |
High performance computing can be used to address important problems related to science and engineering but also for fun. Here was used parallel Navier-Stokes solver to compute the flow around a golf ball traveling at speeds up to 100mph. The computations are amongst the largest Direct Numerical Simulations of complex flows ever performed, involving billions of grid points and thousands of processors on large parallel clusters. Our aim is to illuminate the detailed mechanisms by which the dimples dramatically reduce the drag force on the golf ball over a narrow range of speeds. |
The most realistic way to reduce the drag on a golf ball is to trip the boundary layer. This is done by using dimples, ie creating a rough surface that promotes an early transition to a turbulent boundary layer. This turbulence helps the flow remain attached to the surface of the ball and reduces the size of the separated wake so as to reduce the drag it generates in flight. When the drag is reduced, the ball flies farther. The best way to reduce drag on an object can also depend on the control that can be imposed on the direction of airflow. For an aircraft or a car, airflow direction can, to a greater or lesser extent, be predicted. Extremes of cross flow or reverse flow are not as frequent so are not given the same weight in the process of performance optimisation.
 |
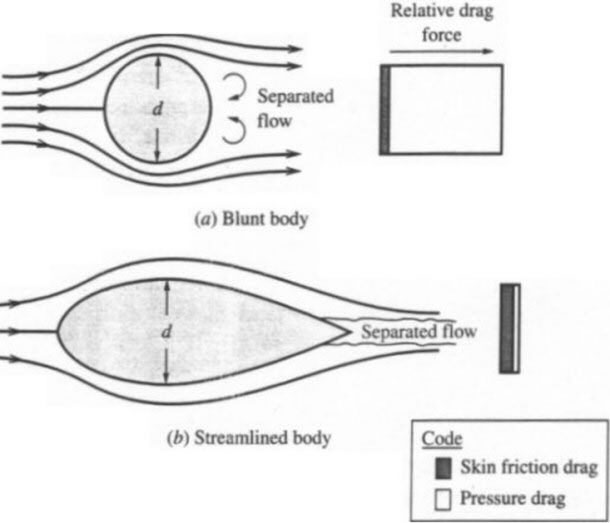Fig 4. Comparison of flow separation and drag on blunt and streamlined shapes |
The reason we do not see dimples on other shapes, like wings, is that these particular forms of boundary layer trips only work well on a blunt body like a sphere or a cylinder. The most dominant form of drag on these kinds of shapes is caused by pressure. More streamlined shapes like the airfoils used on wings are dominated by a different kind of drag called skin friction drag. These streamlined bodies, like that pictured above, have a teardrop shape that creates a much more gradual adverse pressure gradient. This less severe gradient promotes attached flow much further along the body that eliminates flow separation, or at least delays it until very near the trailing edge. The resulting wake is therefore very small and generates very little pressure drag.
However, there do exist other types of devices commonly used on wings that create a similar effect to the dimples used on golf balls. Though these wing devices also create turbulence in order to delay flow separation, the purpose is not to decrease drag but to increase downforce. One of the most popular of these devices is the vortex generator. Vortex generators are often placed along the outer portion of an (aeroplane) wing in order to promote a turbulent boundary layer that adds forward momentum to the flow. As in the case of the golf ball, this turbulent boundary layer helps the flow overcome an adverse pressure gradient and remain attached to the surface longer than it would otherwise. (We have taken parts of this text from the reference indicated here. ****)
For global vehicle performance reasons all the front wing shapes used in F1 now are almost brutally three-dimensional in that the shape is different as you move along the span. These shape changes then create vortices at profile junctions which need to be managed as they move along and around the car. F1 teams employ a number of aerodynamic devices which make virtually no direct contribution to downforce but which create or manage flow features around directly important downforce-generating surfaces thereby enhancing overall performance.*****
It should also be remembered that, in a race, an F1 car is bombarded with sand, stones, insects, balls of rubber and other debris which can change car performance notably.
A lot of research would need to be carried out to find out if and where different types of a surface finish might improve the car. Past experience, including short-term positive experiences with surface finish changes, taught us that revising the shape was more effective than revising the surface finish. Covering a whole vehicle with the any single treatment would not be practical or beneficial. We have invested in this research in the past and spent some money and energy on it again in 2012 but this did not lead to an improvement. From time to time we believe that, due to new information, we have a chance to improve performance in this way. However, so far we have not found permanent improvements using this technique. Most teams in F1 have had the same experience as Sauber.
Willem Toet
February 2013
There are many references relating to this subject that can be found on the internet. We have used some in the creation of this short explanatory document.
REFERENCES:
* Schrauf, 2005
** Polezhaev, Yu.V. & Chircok, I.V., “Drag Coefficient“, DOI: 10.615/AtoZ.d.drag_coefficient, Fig 1, Thermopedia, http://www.thermopedia.com/content/707/?tid=104&sn=1423
*** Bill Pien, Supervisor of Aerodynamics in Ford Vehicle Engineering, October 2009, http://www.popularmechanics.com/cars/news/4316702
**** Jeff Scott, 13 February 2005, http://www.aerospaceweb.org/question/aerodynamics/q0215.shtml; http://www.aerospaceweb.org/about/bios/jeffscott.shtml
***** Toet, W., Aerodynamics and Aerodynamic Research in Formula 1, The Aeronautical Journal, 117, No 1187, January 2013
Back to the top of the page
