Bernoulli's Equation

Daniel Bernoulli (Groningen, January 29, 1700 – July 27, 1782) was a Swiss mathematician who spent much of his life in Basel where he died. A member of a talented family of mathematicians, physicists and philosophers, he is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics. (Wikipedia)
The simplest and most popular explanations of aerodynamic lift invoke the Bernoulli principle, which, in turn, is derived from Bernoulli's theorem. Investigated in the early 1700s by Daniel Bernoulli, his equation defines the physical laws upon which most aerodynamic rules exist. This now famous equation is absolutely fundamental to the study of airflows. Every attempt to improve the way an F1 car pushes its way through molecules of air is governed by this natural relationship between fluid (gas or liquid) speed and pressure. There are several forms of Bernoulli's equation, three of which are discussed, in the succeeding paragraphs: flow along a single streamline, flow along many streamlines, and flow along an airfoil.
All three equations were derived using several assumptions, perhaps the most significant being that air density does not change with pressure (i.e. air remains incompressible). Therefore they can only be applied to subsonic situations.
Being that F1 cars travel much slower than Mach 1, these equations can be used to give very accurate results.
Low speed fluid flow along single or multiple streamlines is interpreted in Figure 1. The presumptions regarding the application of Bernoulli's equation to this scenario are listed in the figure. In this situation, there exists a relationship between velocity, density and pressure. As a single streamline of fluid flows through a tube with changing cross-sectional area, (for example an F1 air inlet), its velocity decreases from station one to two and its total pressure equals a constant. With multiple streamlines, the total pressure equals the same constant along each streamline. However, this is only the case if height differences between the streamlines are negligible. Otherwise, each streamline has a unique total pressure.

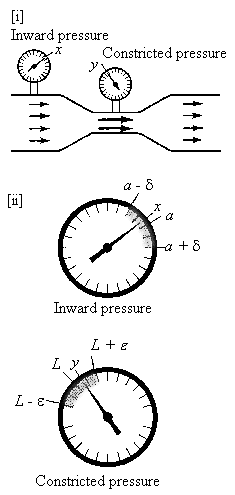
Mathematical and pictorial explanation of Bernoulli's Equation as applied to fluid flow through a tube with changing cross-sectional area.
As applied to flow along low speed airfoils (i.e. F1 downforce wings), airflow is incompressible and its density remains constant. Bernoulli's equation then reduces to a simple relation between velocity static pressure.
(pressure) + 0.5(density)X(velocity)2 = constant
This equation implies that an increase in pressure must be accompanied by a decrease in velocity, and vice versa. Integrating the static pressure along the entire surface of an airfoil gives the total aerodynamic force on a body. Components of lift and drag can be determined by breaking this force down.
In order to discuss lift and downforce, it may be helpful to provide an additional explanation of the relationship that occurs with the above form of Bernoulli's equation. If a fluid flows around an object at different speeds, the slower moving fluid will exert more pressure on the object than the faster moving fluid. The object will then be forced toward the faster moving fluid. A product of this event is either lift or downforce, each of which is dependent upon the positioning of the wing's longer chord length. Lift occurs when the longer chord length is upward and downforce occurs when it is downward.
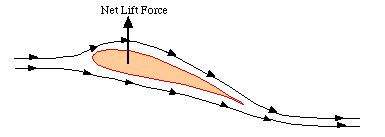
Lift according to the application of Bernoulli's Equation
Though Bernoulli's principle is a major source of lift or downforce in an aircraft or racing car wing, Coanda effect plays an even larger role in producing lift. To know more about interaction of Bernoulli principle and Coanda effect check my article here.
Whilst Bernoulli's principle is often invoked to explain the phenomenon of aerodynamic lift generated by the air flow around a wing profile, there are alternative explanations which employ, in some combination: the 'Coanda effect', the notion of circulation, and Newton's third law. These alternative explanations are, at the very least, equally legitimate to the Bernoulli-principle explanation, and, amongst aerodynamicists, are considered to be superior in some extend to the Bernoulli explanation.
Gordon McCabe issued a great paper on that argument, "Explanation and discovery in aerodynamics" from February 2, 2008. You can download his work from here.
From Abstract:
"The purpose of this paper is to discuss and clarify the explanations commonly cited for the aerodynamic lift generated by a wing, and to then analyse, as a case study of engineering discovery, the aerodynamic revolutions which have taken place within Formula 1 in the past 40 years. The paper begins with an introduction that provides a succinct summary of the mathematics of fluid mechanics."






