Traction circle
To control the car's handling one must control the tire's contact with the ground. There are two main elements that affect the tire's contact with the ground: tire loading and camber.
The traction circle is way of thinking about the grip that a particular tire has on the road, how much of it, and how you can use it.
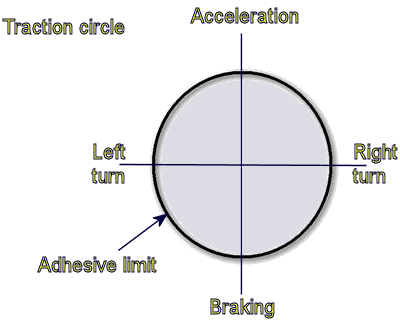
Tires will always provide a given amount of traction. The tire does not care in what direction the force is applied. It only has a given amount of traction. In the picture above you can see a circle, with an x-axis and y-axis running through the center. The edges of the circle denote 100% utilization, the x-axis represents lateral grip (or cornering grip), the y-axis represents longitudinal grip (or braking/accelerating grip). This area in the circle represents the domain of your tire's grip. Points inside the circle are possible combinations of acceleration, braking, and turning; points outside cause the tire to lose grip and slide. If you're a real geek, you'll realize that this is a vector whose magnitude is always less than 1.
Traction circle is a way of teaching people the basics of tire grip, the essential limiting factor in performance driving. In the traction circle, you can be either turning left, turning right, accelerating, braking, or a combination of this. The important thing the traction circle illustrates is that you can combine turning and speeding up or slowing down, but the less of one you do, the more grip for other you have. This explains why you can't go through a hairpin at 100mph, but more importantly, it tells you why you can't go through a 70 kmh turn at 75 kmh. It also helps explain why cornering technique tend to tell you to brake, turn, accelerate rather than to brake through the turn, then accelerate through it. The full radius of the circle is 1 unit. 1 unit is equal to 100% adhesion limit of a tire.
Look at this picture:
 Traction circle
Traction circle
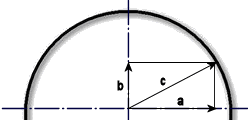
It should help you picture the given amount of traction. A circle where force "a" represents a side force (the centrifugal, cornering force) and force "b" represents acceleration or braking force, but the tire will only handle a given amount of force represented by "c". The circumference of this circle represents given amount of tire traction, 0.8 g or 1.1 g etc. The point is the tire will only handle a given amount of traction, which is a sum of "braking or acceleration" and side force. To prove this mathematically, we can use the Pythagorean Theorem. Draw a right triangle with the horizontal leg representing lateral (turning) acceleration, and the vertical leg representing acceleration/braking force. Using the Pythagorean theorem we can find the hypotenuse. If you try to accelerate too much, or turn at too high of a speed, the tires will skid.
This is how force a and b are summed together to find the overall force c.
Equation for Traction Circle:
![]()
In real situations, a traction circle may be less of a perfect circle, and flattened at one or more axes. For example, a rally car tends to oversteer, so the lower end of the circle may be only .8 units from the center or the tire could have a little more side grip vs. forward grip, or vice versa. But the summing of "a" and "b" to get "c" will still look and be done as explained before.
This given amount of traction is altered by adjusting car settings. Tire loads and camber are just a two of the things that can be changed to change the given amount of traction. The amount of traction is also altered by changes in tire compound, tire treads, track surfaces, etc. But it will always be a given amount of traction at any moment in time. When the given amount of traction "c" is exceeded by the forces acting on the tire, the given amount of traction "c" drops. The size of the circle grows smaller quickly. On asphalt, a thin layer of the tire melts because of the fiction, this layer then acts as a lubricant for the tire to slip on. On dirt, the spikes of the tire will break up the dirt of the track and this loose dirt then acts like bearings for the tire to slip on. On either surface the given amount of traction gets smaller the moment the given amount of traction is exceeded.
For example, you are driving a four wheel drive car though a corner at the car's maximum cornering force. The throttle is positioned so that the car is coasting. Of course it cannot coast for long because of friction, but just for this moment.
Question: What can you do to the throttle to make the car go faster while maintaining the same radius? Answer: Nothing. Whatever you do to the throttle will make the tires break loose. Figure below shows "a" to be the maximum cornering power, because it extends to the circle. The modified throttle position is shown by line "b", it sums with "a" to make force "c" which is clearly outside of the circle. Therefore the tire slips.
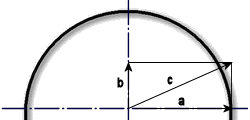
Let's do another example. You are driving a two wheel drive car down a straight. The car is accelerating at the maximum grip the tires will hold, hence the acceleration force extends to the circle. Question: How much steering can you apply? Answer: None. Whatever you do to the steering will make the tires break loose. Figure below shows "b" to be the maximum acceleration force, because it extends to the circle. The modified steering position is shown by line "a", it sums with "b" to make force "c", which is clearly outside of the circle. Therefore the tire slips. The car will spin nearly instantly.

Of course, the best strategy would be to follow very closely to the edge of the traction circle at all times so that one is not taken off guard by sudden changes, but you risk being passed by someone using 98% of their grip. Traction becomes an issue when following behind someone, as you will most likely be forced into the line they choose, so outbraking and pushing the car becomes the strategy to pass. However, because the difference between 100% and 95% is never more than a few seconds at the end of a race, it is more important to focus on cutting good racing lines and following the track than to focus on pushing the car to the 100% limit of grip.
To have a complete picture of performance driving, take a look at Corners, Setup, Using tires, Left foot braking, braking, advanced braking, WRC braking technique, Slipstreaming, drifting, cornering, shifting, Heel and toe driving technique and steering technique articles
Back to the top of the page






